7 problemów milenijnych
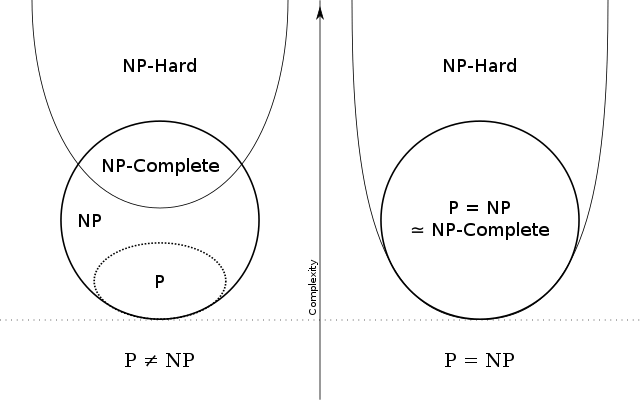
Problem równości klas P i NP
(1971)czy wszystkie pytania, na które odpowiedź – jeśli się ją zna – można zweryfikować w czasie t, rozwiązanie – bez znajomości odpowiedzi – zabierze tyle samo czasu t (mierzonego poprzez złożoność obliczeniową)?
Nierozwiązany. Wielokrotnie przedstawiano próby jej udowodnienia, jak i obalenia, a także wykazania niedowodliwości.

Hipoteza o cyklach Hodge'a
(1950)czy na algebraicznych rozmaitościach rzutowych każdy cykl Hodge'a jest wymierną liniową kombinacją cykli algebraicznych? Hipoteza dotyczy algebraiczności wybranych klas kohomologii de Rhama.
Rozwiązany dla niektórych wersji.

Hipoteza Poincarégo
(1904)każda trójwymiarowa zwarta i jednospójna rozmaitość topologiczna bez brzegu jest homeomorficzna ze sferą trójwymiarową.
Ostatecznie potwierdzona w 2003 roku przez Grigorija Perelmana. Jego prace zweryfikowano w 2006 roku.

Hipoteza Riemanna
(1859)część rzeczywista każdego nietrywialnego zera funkcji dzeta jest równa ½.
Nierozwiązany. Przedstawiono wiele argumentów za jej poprawnością.

Równania kwantowej teorii Yanga-Millsa
(1954)próba opisania jednym formalizmem matematycznym oddziaływania słabego, silnego i elektromagnetycznego.
Nierozwiązany. Powstało wiele nowszych i bardziej skomplikowanych potencjalnych teorii tego typu.
Równania Naviera-Stokesa
(1822)rozwiązania tych równań dla najbardziej skomplikowanych zjawisk hydrodynamicznych.
Istnieją wyniki w szczególnych przypadkach. Brak pełnego rozwiązania.

Problem Bircha i Swinnertona-Dyera
(1960)związany z przewidywaniem rozwiązywalności pewnych równań diofantycznych związanych z krzywymi eliptycznymi.
Rozwiązany dla niektórych wersji.

Grigorij Perelman
Grigorij Jakowlewicz Perelman, ros. Григорий Яковлевич Перельман – rosyjski matematyk, były profesor Instytutu Stiekłowa w Petersburgu. Udowodnił hipotezę geometryzacyjną Thurstona, i tym samym wypływającą z niej jako wniosek hipotezę Poincarégo – jeden z problemów milenijnych.
W grudniu 2005 porzucił stanowisko głównego pracownika naukowego laboratorium fizyki matematycznej, odszedł z Instytutu i praktycznie całkowicie zerwał kontakty z kolegami. Od tamtej pory nie wykazywał zainteresowania karierą naukową. Na Międzynarodowym Kongresie Matematyków, który odbywał się od 22 do 30 sierpnia 2006 w Madrycie, Perelman został jednym z laureatów Medalu Fieldsa.
John M. Ball, przewodniczący Międzynarodowej Unii Matematycznej poinformował, że Perelman odmówił przyjęcia medalu. W marcu 2010 za udowodnienie hipotezy Poincarégo Instytut Matematyczny Claya przyznał mu jedną z siedmiu Nagród Tysiąclecia w wysokości miliona dolarów, jednak Perelman odmówił jej przyjęcia w lipcu 2010 roku.
Obecnie mieszka wraz z matką w Sankt Petersburgu, w niewielkim mieszkaniu w bloku. Prowadzi ascetyczny tryb życia, unika kontaktów z mediami. W rosyjskiej prasie były podawane też informacje o jego zatrudnieniu w Szwecji od 2014 roku.
7 problemów milenijnych
Zestaw siedmiu zagadnień matematycznych ogłoszonych przez Instytut Matematyczny Claya 24 maja 2000 roku.